「水圧って何?そもそも圧力すら分からない…」
「浮力の計算が理解できないからおしえて!」
中3理科の浮力・水圧は、多くの生徒が苦手意識を持つ分野です。
計算問題は浮力と水圧の両方の理解が必要で、テストや入試で差がつくポイントでもあります。
そこで、現役教師である私が、徹底的に分かりやすく解説します。
基本や実験、練習問題をとおして、徹底的にやさしく解説します。
浮力と水圧は、解くコツさえ分かれば、得意分野にすることも可能です。
【水圧のしくみ】深いほど大きくなる
私たちの身のまわりでも影響を与えている水圧には、次のようなしくみと性質があります。
【水圧とは】
- 水圧 = 水中の物体が水から受ける圧力
- 深いところほど大きくなる
※同じ深さでは、あらゆる向きに同じ大きさではたらく
この後、水圧のしくみや性質について詳しく解説しますね。
水圧とは?水の重さによる力
水圧(すいあつ)とは、水中の物体がまわりの水から受ける圧力のことです。
プールに深くもぐったときに感じる、体全体にかかるような水のはたらきが、まさに水圧。
水圧は、ある深さにおいて、その地点より上にある水の重さによって生じる圧力です。
深くなるほど、上にある水の量が増え、その重さが増すため、水圧も大きくなるのです。
水圧には、次の重要な性質があります。
【水圧の性質】
- 深いところほど大きくなる
- 同じ深さでは、あらゆる向きに同じ大きさではたらく
実験で分かる水圧の性質
水圧がどのようにはたらくのかを、確認できる実験があります(下図)。
上図のように、水槽に水を入れた状態で、ゴム膜を張った筒を沈めます。結果は次のようになります。
【結果】
- 筒を深く沈めるほど、ゴム膜は内側に大きくへこむ
- 同じ深さで筒の向きを変えても、ゴム膜のへこみ方は変わらない
この実験で分かる水圧の性質は、次の2点です。
【実験で考察される水圧の性質】
- 深いところほど水圧が大きくなる
- 水圧はあらゆる向きに、同じ大きさではたらく
【復習】力や圧力のしくみ
水圧の理解を深めるために、1年で学んだ力(ちから)、2年で学んだ圧力(あつりょく)について復習しておきましょう。
力(ちから)とは
力は、物体を動かすなどできるはたらきのことです。力には、
【力のはたらき】
- 物体の形を変える
- 物体の動き(速さ・向き)を変える
- 物体を支える
という、3つのはたらきがあります。
力の単位はN(ニュートン)で表されます。
100gの物体にはたらく地球上での重力の大きさは、およそ1Nです(正確には0.98N)。
【力の求め方】
100g=1Nとすると、1kg= 10N
ばねのように、変形した物体が元に戻ろうとする力は弾性力と呼ばれます。フックの法則(ばねののびは、ばねにはたらく力の大きさに比例する)も、力と変形の関係を表す重要な法則です。
圧力(あつりょく)とは
圧力は、単位面積あたりにはたらく力の大きさのことです。どれくらいの力が、どれくらいの面積に集中してはたらいているかを示します。
圧力の単位にはPa(パスカル)が用いられ、1 Pa = 1 N/m²(ニュートン まい 平方メートル)です。
【圧力の公式】
- 圧力[Pa] = 圧力[N/㎡]
= 面に垂直にはたらく力[N] ÷ 力を受ける面積[㎡] - 1 Pa = 1 N/㎡
- 1 hPa(ヘクトパスカル) = 100 Pa
はたらく力が同じでも、力を受ける面積が小さいほど、圧力は大きくなります。
【浮力のしくみ】深くても浅くても変わらない
ものの浮き沈みに関係がある浮力(ふりょく)には、次のような性質があります。
【浮力とは】
- 浮力=水中の物体に水からはたらく上向きの力
- 浮力の大きさは、水中の物体の体積の大きさで決まる
- 浮力の大きさは、物体を沈める深さに関係しない
- 物体の浮き沈みは、重力と浮力の大小関係で決まる
この章では、浮力のしくみと、水圧との関係、具体的な浮力の計算方法について詳しく解説します。
浮力とは?水圧の差により生じる力
浮力とは、水中の物体に水からはたらく上向きの力のことです。
なぜ浮力が生まれるのでしょうか?その答えは、水圧の差にあります。
物体を水中に沈めると、その物体にはあらゆる方向から水圧がはたらきます。ここで大切なのは深いところほど水圧が大きいという点です。
- 物体の上面では、浅いところの水圧が下向きにはたらく
- 物体の下面では、深いところの水圧が上向きにはたらく
「下面にはたらく上向きの水圧」と「上面にはたらく下向きの水圧」の間に力の差が生まれます。この力の差が、物体を上向きに押し上げる力「浮力」となるのです。
上面と下面との間を長くすると、より大きな差が生まれ、浮力が大きくなります。つまり、浮力の大きさが物体が水に沈んでいる部分の体積によって決まることがわかります。
沈んでいる部分の体積が同じであれば、上面と下面の水圧の差は変わらないため、深く沈めても浅く沈めても浮力の大きさは変わらないのです。
浮力の性質をまとめると次のとおりです。
【浮力の性質】
- 物体が水に沈んでいる部分の体積が大きいほど、浮力は大きくなる
- 浅く沈めても深く沈めても、浮力は変わらない
- 物体が浮くか沈むかは、重力と浮力の大小関係で決まる
【公式】浮力の求め方
浮力の大きさは、下図のようにばねばかりを使った簡単な実験で求められます。
まず、物体を空気中でばねばかりにつるすと、ばねばかりは物体にはたらく重力の大きさを示します。
次に、物体を水中に完全に沈めると、ばねばかりの値は小さくなります。これは、物体には「重力」と「ばねばかりが引く力」に加えて、上向きに浮力がはたらいているためです。
物体が水中で静止しているとき、物体にはたらく3つの力はつり合います。
【水中の物体にはたらく力のつり合い】
- 下向きの力: 重力(空気中でのばねばかりの示す値)
- 上向きの力: 水中でばねばかりが引く力(水中で示す値)+ 浮力
この関係は、次の式で表すことができます。
重力 = 水中でばねばかりが引く力 + 浮力
上の式から、浮力を求める公式が分かります。
【浮力の公式】
浮力(N) = 空気中での重さ(N) − 水中での重さ(N)
つまり、空気中での重さと水中での重さの差がそのまま浮力の大きさになるのです。
実験で分かる浮力の大きさ
浮力の大きさを測定する2つの実験をとおして、浮力の性質を解説します。
実験1:浮力の大きさと、物体の深さや質量との関係
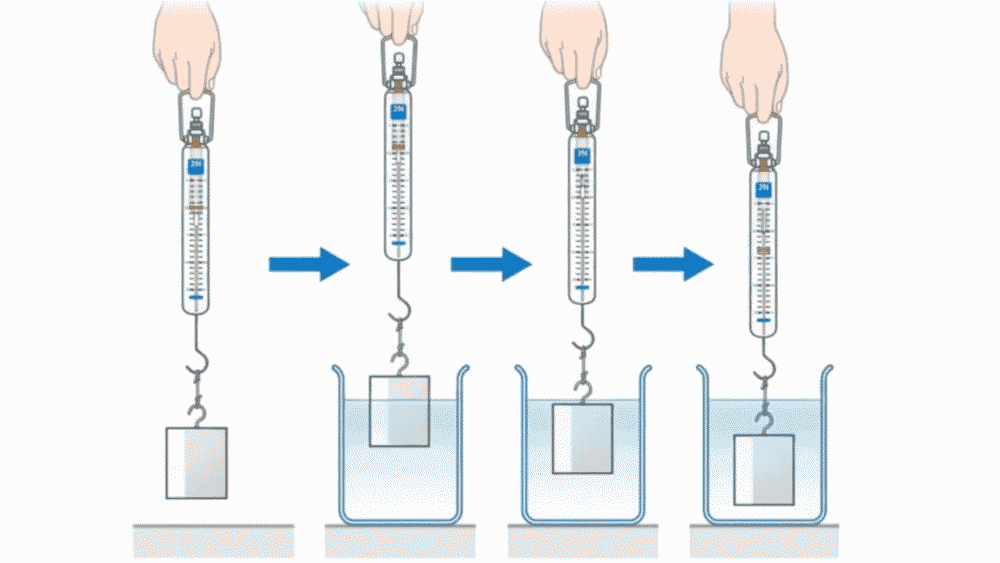
上図のような装置と、質量の異なる2つのおもり(小)とおもり(大)を使って、次の手順で実験を行います。
【実験手順】
- おもりをばねばかりにつるし、空気中での重力をはかる
- おもりを少しずつ水中に沈め、半分水中、水中(浅い)、水中(深い)でのばねばかりの値を記録する
実験の結果の例は、下の表のようになります。
【実験結果の例】
| 空気中 (N) | 半分水中 (N) | 水中(浅い) (N) | 水中(深い) (N) | |
| おもりA | 0.45 | 0.40 | 0.35 | 0.35 |
| おもりB | 0.80 | 0.70 | 0.60 | 0.60 |
上記の結果より、次のことが考察できます。
【実験の考察】
- 水中では、物体に上向きに浮力がはたらいている
[理由]ばねばかりが示す値が、物体が水中にあるときの方が、空気中にあるときよりも小さくなっているため - 水中に沈む体積が増えるほど、浮力が大きくなる
[理由]おもりが半分だけ沈んでいる状態よりも、完全に沈んでいる状態のほうが、ばねばかりの値が小さくなっているため - 浮力の大きさは、水中に沈んでいる深さには関係しない
[理由]おもりが完全に沈んでいる状態であれば、「水中(浅い)」でも「水中(深い)」でも、ばねばかりが示す値が同じであるため
実験2:浮力の大きさと、物体の体積や質量との関係
★実験図を挿入★
上図のような装置と、同じ質量で体積の異なる2つの容器をつかって、次の手順で実験を行います。
【実験手順】
- メスシリンダーを用いて、それぞれの容器の体積をはかる
- ばねばかりを用いて、空気中での容器の重力をはかる
- 2つの容器を同じ深さまで水中に沈め、ばねばかりの値を記録する
- 「空気中での重力」から「水中での重力」を引いて、浮力を計算する
実験2の結果の例は、下の表のようになります。
【実験結果の例】
| 体積(㎤) | ①空気中の重力(N) | ②水中の測定値(N) | 浮力(N) = ①ー② | |
| 容器(小) | 80 | 1.5 | 0.7 | 0.8 |
| 容器(大) | 135 | 1.5 | 0.1 | 1.4 |
上記の結果より、次のことが考察できます。
【実験の考察】
- 体積が大きいほど、浮力は大きくなる
[理由]重力が同じ容器であっても、体積が大きい容器の方が浮力が大きくなっているため - 浮力は、物体の質量には関係しない
[理由]2つの容器は重力(質量)が同じなのに、浮力が異なっているため
【テスト対策】浮力と水圧の計算のコツ
浮力と水圧の問題は、テストでよく出るため重要です。
次のポイント・公式をしっかり押さえましょう。
- 水圧性質:水圧は、浅いとき小さく、深いとき大きい
- 浮力性質①:物体の水中部分の体積が大きいほど、浮力は大きい
- 浮力性質②:完全に水中に沈めると、深くても浅くても浮力は変わらない
浮力(N) = 空気中での重力(N) ー 水中での重力(N)
上記のポイントと公式を使いこなして、例題に挑戦してみましょう。
【問い】ばねばかりに物体をつるすと、空気中のAでは0.8N、水中に完全に沈めた状態のCでは0.3Nを示した。
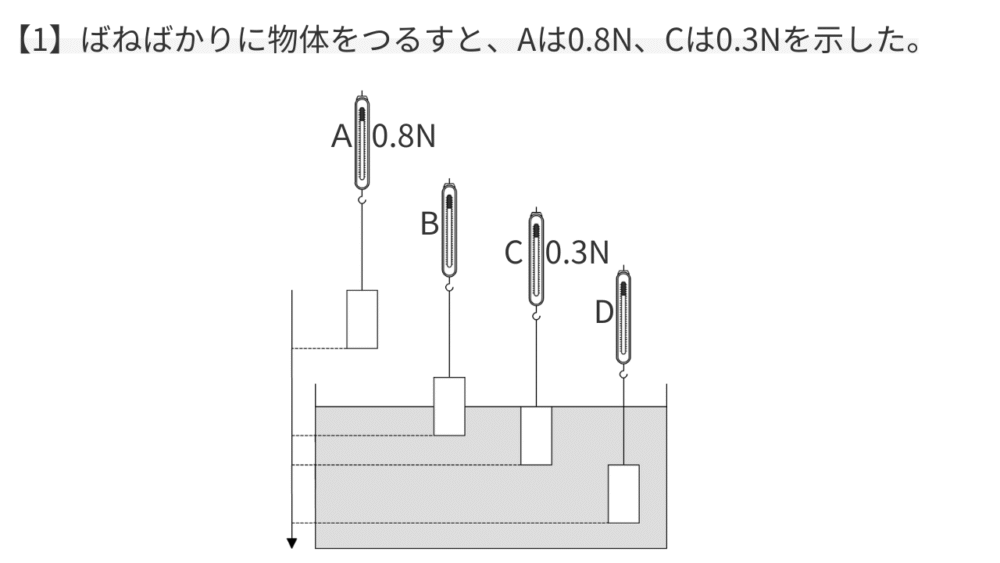
例題1:水圧を比べる
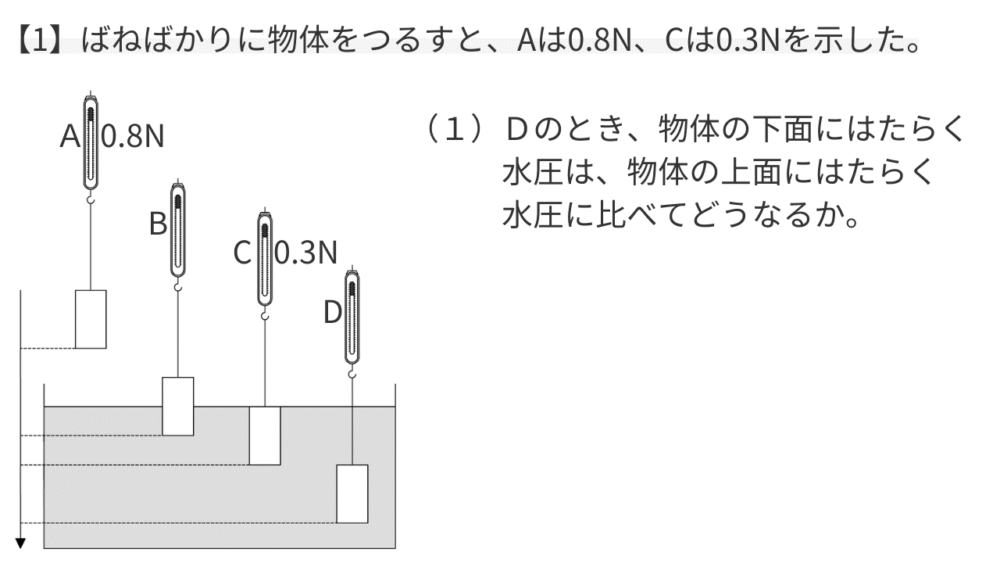
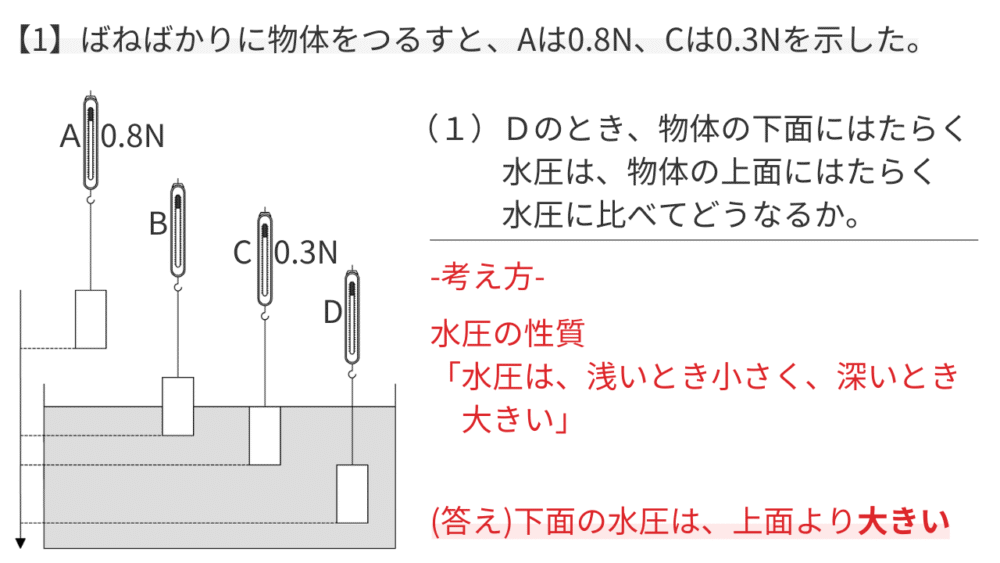
【考え方】
水圧の性質「水圧は、浅いとき小さく、深いとき大きい」という基本を思い出しましょう。
【答え】
![]()
【例題2】完全に沈んでいる物体の浮力を求める
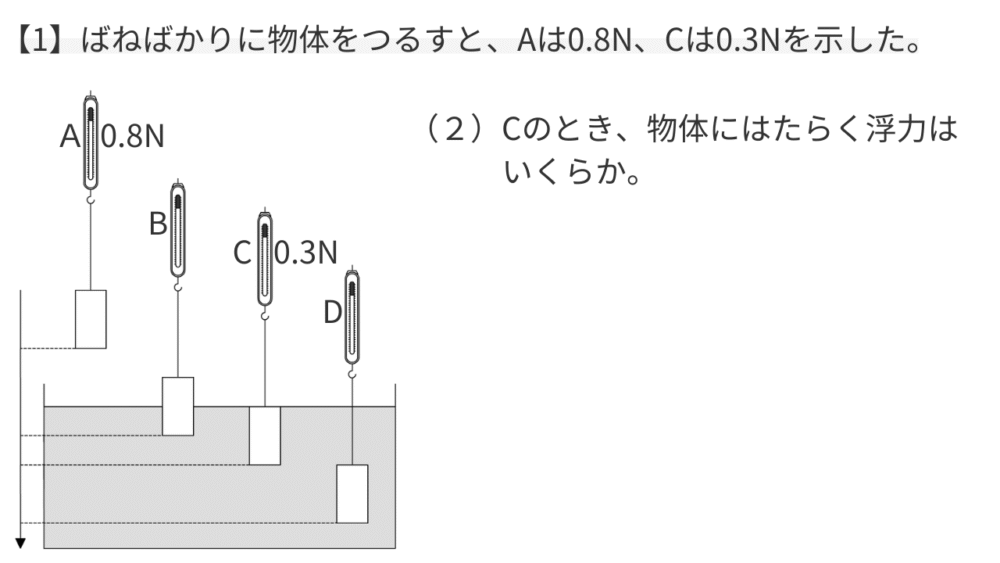
【考え方】
浮力の公式「浮力=空気中の重力ー水中での重力」に数値を当てはめて計算します。
- 空気中の重力:0.8N
- 水中の重力:0.3N
浮力=0.8(N)ー0.3(N)=0.5(N)
【答え】
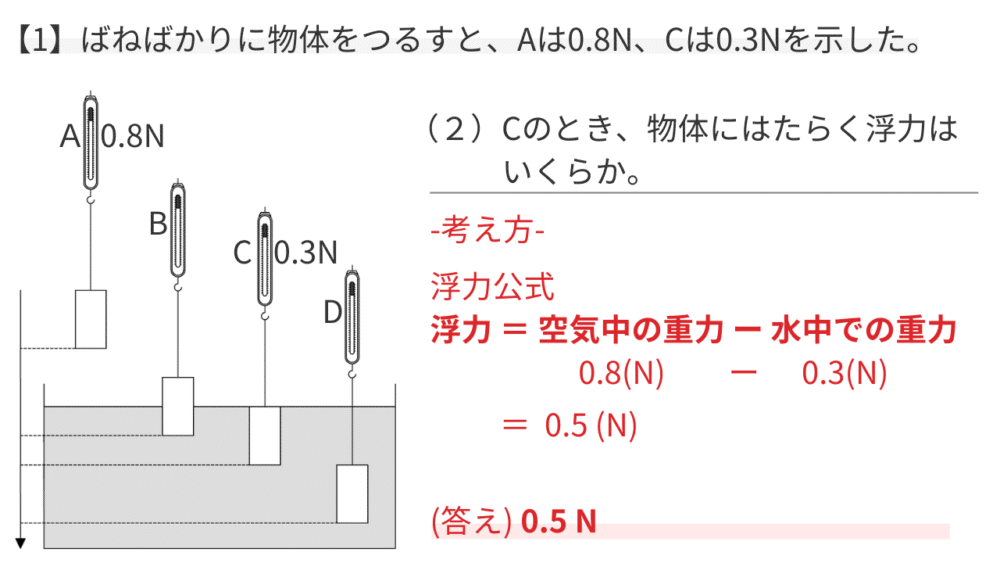
【例題3】空気中に出ている部分がある物体の浮力を求める
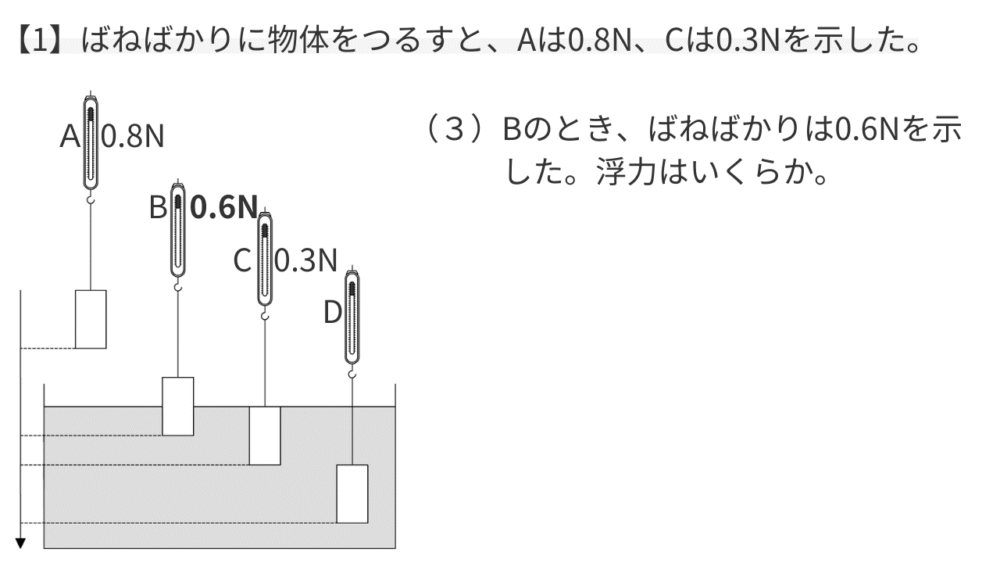
【考え方】
浮力の公式「浮力=空気中の重力ー水中での重力」に数値を当てはめて計算します。
- 空気中の重力:0.8N
- 水中の重力:0.6N
浮力=0.8(N)ー0.6(N)=0.2(N)
【答え】
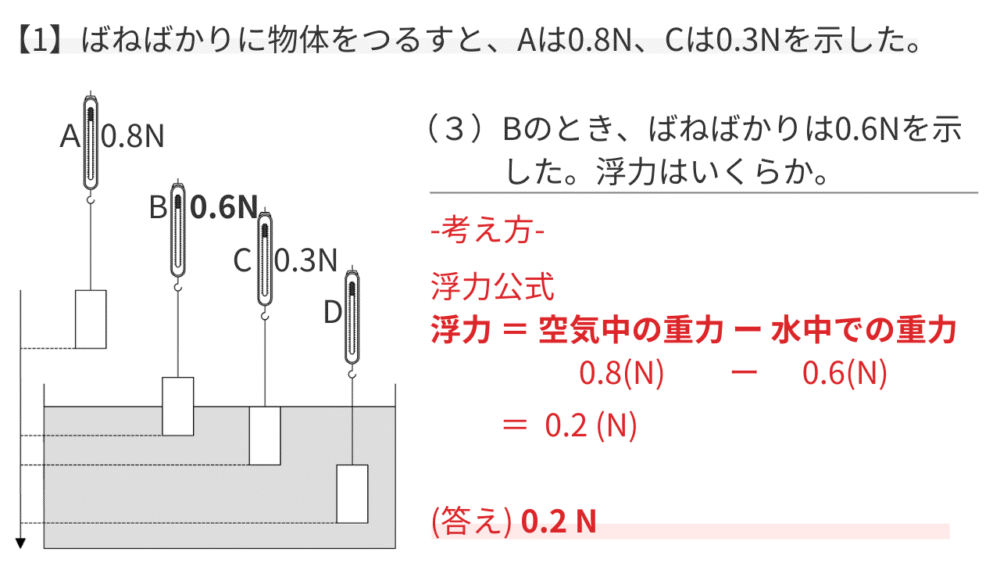
【例題4】浮力を比べる
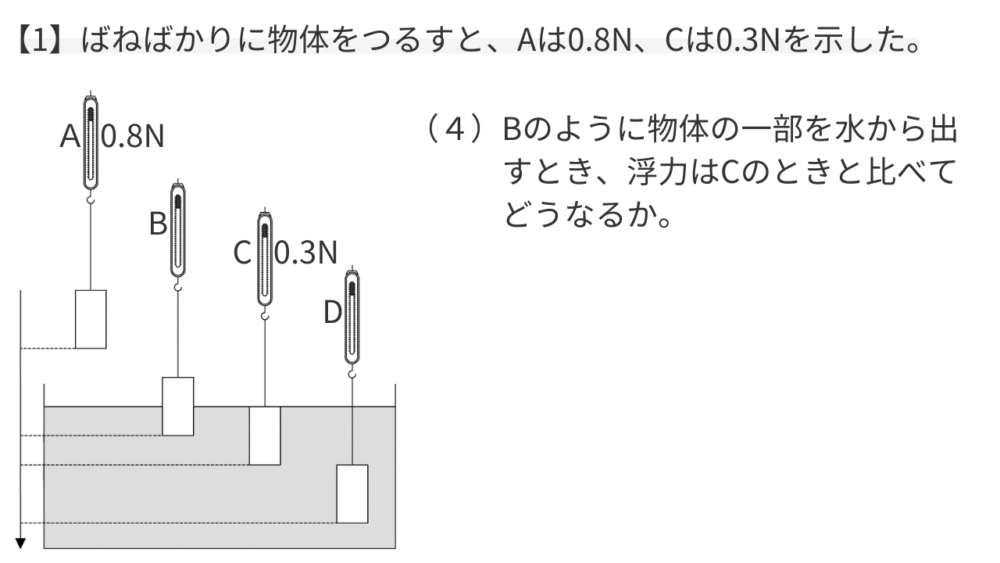
【考え方】
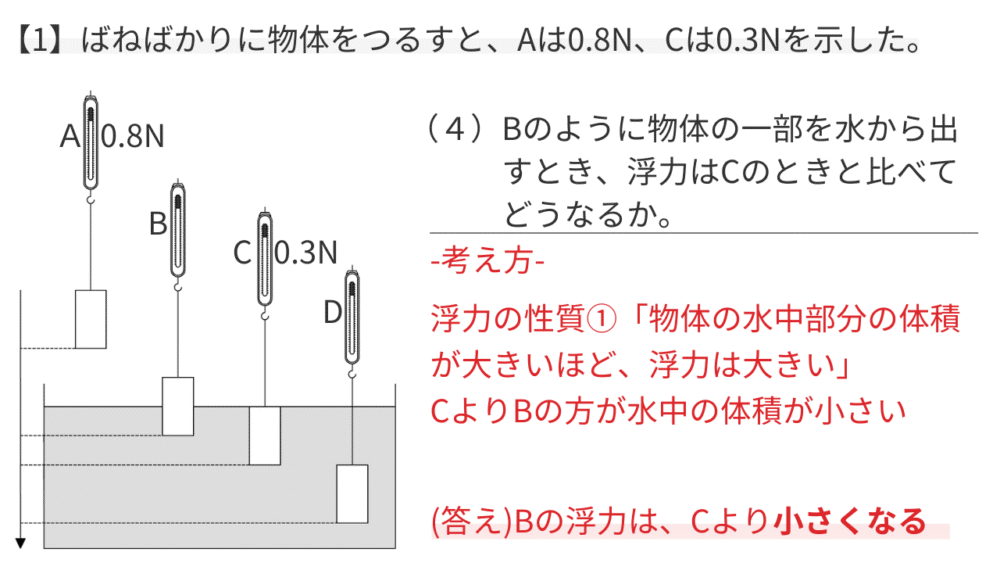
浮力の性質①「物体の水中部分の体積が大きいほど、浮力は大きい」を使います。
Cに比べて、Bは水中に沈んでいる体積が小さいです。
【答え】
【例題5】浮力の深さによる変化を問う
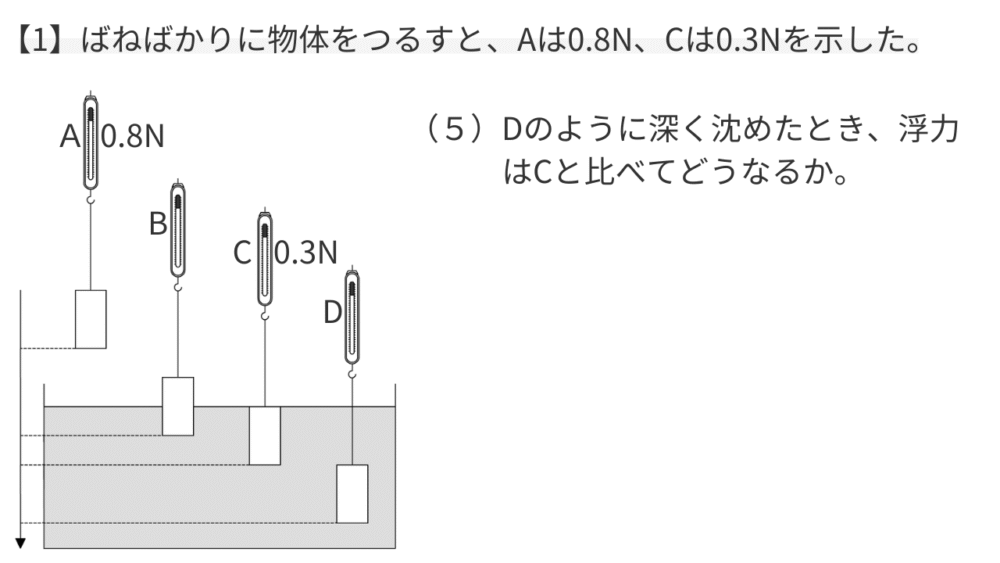
【考え方】
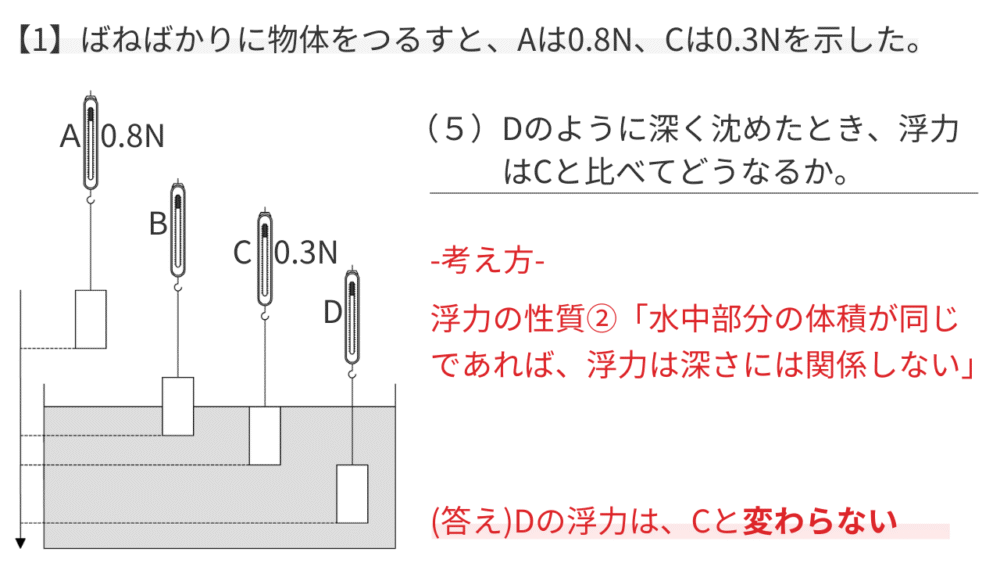
浮力の性質②「水中部分の体積が同じであれば、浮力は深さには関係しない」を使います。
CもDも、物体は完全に水中に沈んでいて、水中の体積が同じです。
【答え】
【例題6】体積を比べる

【考え方1】
- 物体XとYの空気中での重力を求める(400g = 4N)
- それぞれの浮力を計算する
・物体Xの浮力:4N − 2N = 2N
・物体Yの浮力:4N − 3N = 1N - 浮力の性質①「浮力が大きいほど、水中部分の体積も大きい」を使う
【考え方2】
XはYより、水中のばねばかりの値が小さいです。
つまり、Xは水から大きな上向きの力を受けていることが分かります。
その上向きの力が浮力なので、XはYより浮力が大きいと言えます。
ここで、浮力性質①「物体の水中部分の体積が大きいほど、浮力は大きい」を使います。
浮力の大きな物体Xの方が、体積は大きいことがわかります。
【答え】

【まとめ】浮力と水圧の重要ポイント
この記事では、浮力・水圧について学びました。
最後に、必ず押さえておきたい3つのポイントをおさらいしましょう。
- 水圧は「深さ」に注目!
水圧は、浅いとき小さく、深いとき大きい。 - 浮力は「沈んだ体積」に注目!
・物体の水中部分の体積が大きいほど、浮力は大きい。
・完全に沈んでいれば、深さが変わっても浮力は変わらない。 - 浮力の公式を覚える!
浮力(N) = 空気中の重力(N) ー 水中での重力(N)
上記の3つのポイントをしっかり理解していれば、どんな問題が出ても大丈夫です。
下の練習問題にチャレンジして、自分の実力を確かめてみてください。
上の練習問題がよく分からなかった方は、この記事を何度も読み返して、しっかり理解しましょう。








