「合力をかくための平行四辺形ってどうかくの?」
「分力の作図がさっぱり理解できない!」
中3理科の力の合成・分解のうち、特に作図は多くの生徒が苦手とする分野です。
作図問題は三角定規をつかいこなす必要があり、テストや入試で差がつくポイントでもあります。
そこで、現役教師である私が、この作図のコツを徹底的に分かりやすく解説します。
この記事では、力の合成と分解でつまずきやすいポイントを、具体的な作図方法も含めてていねいに解説します。
合力と分力は、書くコツさえ分かれば、得意分野にすることも可能です。
【力の合成】作図のコツを解説
この章では、複数の力を1つにまとめる合力(ごうりょく)の考え方と、テストで差がつく作図のコツを解説します。
合力とは?2つの力が合わさった力
合力とは、物体にはたらく複数の力と同じはたらきをする1つの力のことです。
合力を求めることを力の合成といいます。
合力のイメージをつかむために、2人が同じ方向に本を押す場合を考えてみましょう。
2人が本を押す力は、足し合わされて1つの合力として本にはたらきます。
次に、2人が反対方向に物体を押す場合を考えます。
上図のように、一直線上で反対向きに2つの力がはたらくとき、力の大きさの差が合力の大きさになります。
では、複数の力が一直線上になく角度をもってはたらく場合はどうでしょうか?この場合は、単純に足し算や引き算はできません。
ここで登場するのが、算数・数学で学習した平行四辺形です。
この考え方は、かつて力の平行四辺形の法則とも呼ばれ、力の合成において重要なルールです。
合力の求め方をまとめると、次のようになります。
- 一直線上で同じ向きにはたらく2力:
合力の大きさは、2力の大きさを足し算して求める - 一直線上で反対向きにはたらく2力:
合力の大きさは、2力の大きさを引き算して求める - 角度をもってはたらく2力:
2力の合力は、2力の矢印を2辺とする平行四辺形の対角線として求める
合力を求める実験2例を解説
テストでよく出題される、力の合成を確かめる実験例を2つ解説します。
実験1|角度をもった2力でおもりを引く
この実験は、角度をもってはたらく2力の合力と、もとの2力の関係を調べることが目的です。
【実験手順】
- 2つのばねばかりでリングを点Oまで引き、ばねばかりの値(F1、F2)と、引く力の向きを記録する

- 1つのばねばかりで、リングを同じ点Oまで引き、ばねばかりの値(F3)と、引く力の向きを記録する

- 2つのばねばかりで引く角度を変え、手順①と②をくり返す
- 記録した力の大きさと向きを、記録用紙に矢印でかく
【結果の例】
1回目の結果の例は次の表のとおりです。
| 力F1 | 力F2 | 力F3 |
| 0.63N | 0.3N | 0.8N |
2回目の結果の例は次の表のとおりです。
| 力F1 | 力F2 | 力F3 |
| 0.50N | 0.50N | 0.8N |
実験結果から、次のことが分かります。
【実験の考察】
- 力F3は、力F1とF2の合力である;
[理由]力F3は、力F1・F2の2力でおもりを支える力と同じはたらきをしているため - 力F1、F2、F3の矢印の先と、点Oの4点を結ぶと、平行四辺形ができた

- 角度をもってはたらく2力の合力は、その2力を表す矢印を2辺とする平行四辺形の対角線で表される

- 平行四辺形の対角線の長さが合力の大きさを、対角線の向きが合力の向きを示している
実験2|角度をもった2力でおもりを持ち上げる
この実験は、物体に角度をもってはたらく2力の向きと大きさとの関係を調べることが目的です。
【実験手順】
- 1本のばねばかりで物体をつり下げ、値を記録する
- 2本のばねばかりで物体をつり下げ、真上に物体を引くようにして、ばねばかりの値を記録する
- 重力方向の延長線と、それぞれのばねばかりとの角度、力の大きさをはかり、記録する
- 点Oを作用点とし、物体にはたらく重力、重力とつりあう力、ばねばかりで引く2つの力を矢印でかく
【結果と考察】
実験の結果例は下図のとおりです。
上記の結果から次のようなことが考えられます。
【結果と考察】
- 手順1で記録した1本のばねばかりの値が、物体にはたらく重力の大きさ。
- 手順2で物体を真上に引いた場合、2力の大きさの和が、重力とつり合う力と同じ大きさ。つまり、2力の合力が重力とつり合う力だと分かる。

- 2本のばねばかりで引く角度が大きくなるほど、それぞれの力の大きさは大きくなる。つまり、2力の角度を小さくすると、引く力を小さくできる。

- 物体にはたらく重力とつりあう力(=2力の合力)が、2力を2辺とする平行四辺形の対角線になっている
合力の作図|三角定規で平行四辺形の対角線をかくコツ
図形の作図が苦手な方向けに、絶対に失敗しない平行四辺形の書き方をお伝えします。
定期テストや入試で三角定規の持ち込みが許可されている方は必見の「ヨット法」。三角定規2つをヨットに見立ててもつ方法です。
一方の定規は「船体」として固定する役割、もう一方の定規は「帆・柱」としてスライドする役割にします。
ヨットのうち、線をかくために矢印にあてる「柱」を意識しましょう。
補助線はなるべく長めにかいておくと、あとの作業がラクになります。
2つめの辺も同じ方法で平行線(補助線)を引きます。
補助線は、平行四辺形をつくることを意識して長めにすると、対角線を引きやすくなります。
合力を作図する問題では、作用点(矢印の出発点)を書き忘れないようにしましょう。
例題|合力を求める作図に挑戦
力の合成は、作図のルールさえおさえれば簡単です。作図問題に挑戦してみましょう。
例題1:同一直線上の2力を合成する
【問題】下図のような、同一直線上にある2つの力を合成しましょう。
【作図ステップ】
- 矢印が同じ向きか、反対向きかを確認
- 同じ向きの力は、2力の大きさを足す
- 反対向きの力は、2力の大きさを引く
- 合力の向きと大きさが分かったら、作用点から矢印をかく
【答え】
例題2:角度を持った2力を合成する
【問題】下図のような、角度を持った2つの力を合成してみましょう。
【作図の手順】
- 2つの力(矢印)が作用点から出ていることを確認
- 2つの矢印を隣り合う2辺として、平行四辺形を作図
- 作用点から、作図した平行四辺形の対角線をかく
- この対角線が「合力」となるので、忘れずに矢印(➡)をかく
方眼のマス目を利用すれば、定規を使わなくても簡単に平行線が引けます。
【答え】
【3力のつり合い】
3力のつり合いとは?
1つの物体に3方向から力を加えて静止しているとき、3力はつり合っているといいます。
これは、となり合う2力の合力と、もう1つの力がつり合っているためです。
1年生で学習した2力のつり合いについて復習しておくといいでしょう▼
例題|3力のつり合い
3力のつり合いでは、下図のように3本の矢印が書かれていて、そのうち2本の矢印の合力を作図するパターンが多いです。例題を解いてみましょう。
【例題1】①の図で、力F3とつり合う、力F1とF2の合力を作図せよ。
【考え方】F1とF2を2辺とする平行四辺形をつくり、点Oを作用点とする対角線をかきましょう。
【例題2】②の図で、力F2とつり合う、力F1とF3の合力を作図せよ。
【考え方】F1とF3を2辺とする平行四辺形をつくり、点Oを作用点とする対角線をかきましょう。
【例題1と2の答え】
【力の分解】1つの力を2つに分ける作図方法
分力とは?力を分解するしくみ
力の分解とは、1つの力と同じはたらきをする2つの力に分けることです。
分解してできた力を、もとの力の分力といいます。
「力の分解」は「力の合成」の逆の考え方です。
- 力の合成:2つの力 → 1つの力(合力)
- 力の分解:1つの力 → 2つの力(分力)
力の分解では、もとの力を対角線とする平行四辺形をかくと、そのとなり合う2辺が分力になります。
分力には、次の大切な性質があります。
- 分解する方向が変わると、分力の大きさと向きも変わる
- もとの力と、1つの分力の大きさと向きが分かれば、もう一方の分力も作図できる
分力の作図|平行四辺形を書くコツ
分力の作図は、大きく分けて2つのパターンがあります。それぞれの作図のコツを覚えましょう。
【分力の作図問題パターン】
- 2方向が指定されている問題
※斜面上の物体にはたらく重力もふくむ - 1つの分力が指定されている問題
パターン1:分解する2方向が指定されている
このパターンでは、もとの力を、問題で指定された2つの方向に分解します。
【作図ステップ】
- 分解する2方向の傾きをマス目から読みとる
- 矢印の先を通る、平行な補助線を2本かく
- 平行四辺形の2辺となるように分力の矢印を2つかく
平行四辺形の対角線がもとの力になることを意識しながら作図すると、間違いをふせげます。
パターン2:1つの分力が指定されている
このパターンは、もとの力Fと、一方の分力F₁が示されているときに、もう一方の分力F₂を作図する問題です。
【作図ステップ】
- もとの力Fと、分力F₁の先端どうしを結ぶ補助線をかく
- マス目を読み、補助線の傾きと長さを確認する
※傾き[縦○マス→横○マス]が○セット分の長さあるのか、を確認する - 作用点から補助線と同じ傾き・長さの分力F₂の矢印をかく
例題|分力を求める作図に挑戦
力の分解は、力の合成の逆を考えるだけなので、実は慣れれば簡単です。例題に挑戦して作図の練習をしましょう。
例題1:指定された方向の分力を作図する
【問題】下図のように、指定された2方向に力を分解してみましょう。
【答え】
例題2:1つの分力が指定されている
【問題】下図のように、点Oにはたらく力Fと、その分力の一つである分力F₁が指定されています。もう一方の分力F₂を作図してみましょう。
【答え】
力の合成・分解で考える『浮力・斜面』
力の合成・分解は、次の2つの現象を考えるときに応用される、重要な考え方です。
- 水中の物体にはたらく浮力【力の合成】
- 斜面上の物体にはたらく重力【力の分解】
浮力|浮力と力の合成の関係
水中の物体には、さまざまな方向から水圧がはたらいています。
水圧が生み出す力のうち、上向きと下向きの力に注目してみましょう。
- 上面:下向きに押す、水圧による力
- 下面:上向きに押す、水圧による力
水深が深くなるほど、水圧は大きくなります。
下面にかかる上向きの力は、上面にかかる下向きの力よりも大きくなります。
水圧による上向きの力と下向きの力の合力こそが浮力なのです。
浮力とは水圧の差によって生じる力であり、その大きさは物体の体積(水に沈んでいる部分)によって決まります。
浮力と物体の重力を比べることで、物体が浮くか沈むかを説明できます。
【物体の浮き沈みと浮力の関係】
- 浮力と重力がつり合うとき:物体は静止する
- 浮力の方が大きいとき:物体は浮く
- 重力の方が大きいとき:物体は沈む
浮力と重力の関係は、密度で考えるとより分かりやすくなります。
- 水の密度 > 物体の密度:浮く(例:水に浮かぶ氷)
- 水の密度 < 物体の密度:沈む(例:水に沈む鉄)
斜面|平行・垂直方向に重力を分解
力の分解は、斜面上の物体がすべり下りる理由を説明するのに必要な考え方です。
地球上のすべての物体は、地球の中心に向かって(鉛直下向きに)重力がはたらきます。
斜面上の物体にも、下向きに重力がはたらきますが、移動の方向は真下ではなく、斜面に沿った方向ですね。
斜面上の物体にはたらく重力のように力の向きと移動の向きが異なる場合、次の2方向に分解すると、物体の運動が考えやすくなります。
- 斜面に平行な向き
- 斜面に垂直な向き
重力を斜面に平行・垂直の2方向に分解する方法は次のステップ。
- 重力の矢印をかく。これが分解する前の「もとの力」
- 重力の作用点を通るように、斜面に平行な補助線と、斜面に垂直な補助線をかく
※斜面が縦1・横2の傾きなら、斜面の垂直な補助線の傾きは縦2・横1のように逆になる - 平行四辺形をつくり、2方向の分力の矢印をかく
- 平行四辺形が長方形であり、重力が長方形の対角線になっていることを確認する
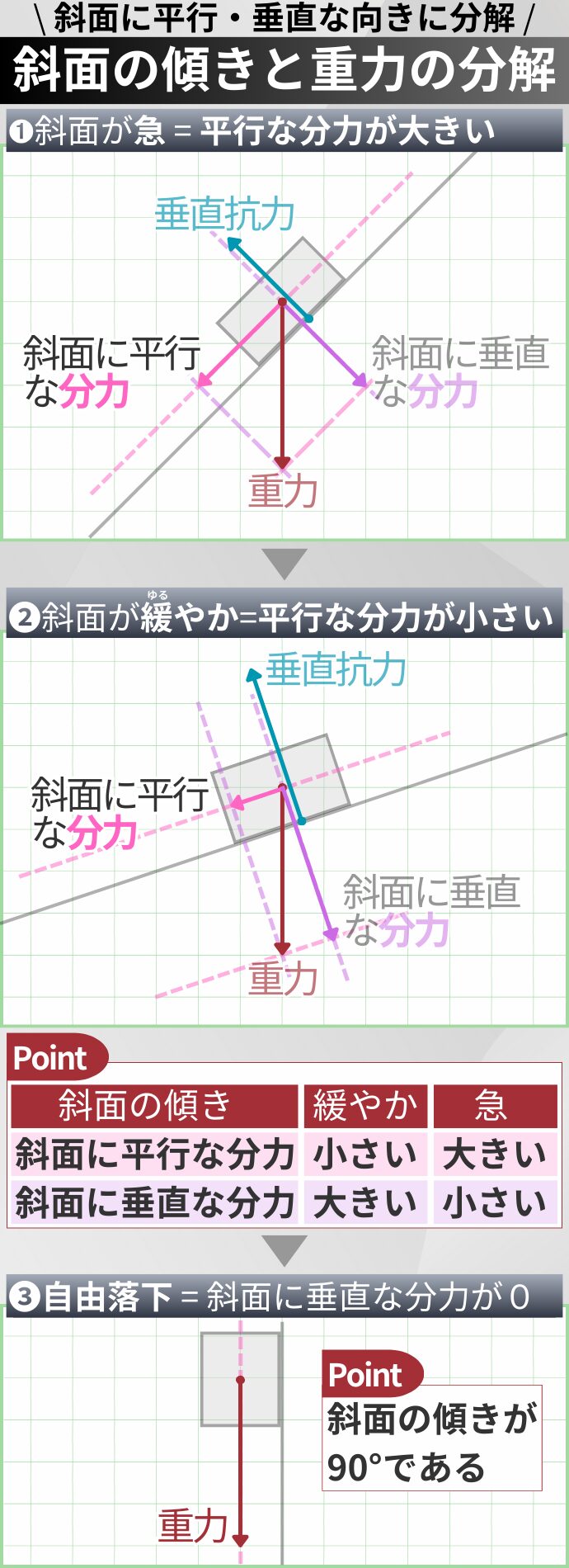
斜面の傾きが変わると、重力を分解したときの2つの分力の大きさも変わります。
- 傾きが急な斜面:斜面に平行な分力が大きい。物体は速くすべる
- 傾きがゆるやかな斜面:斜面に平行な分力が小さい。物体はゆっくりとすべる
斜面の傾きが急な斜面をすべり下りる物体の運動は、速さの増え方が大きくなります。詳しくは次の記事を参考にしてください。
極端な例として、斜面の傾きが90°(地面に対して垂直)になった場合を考えてみましょう。
物体は斜面に平行な分力のみを受け、垂直な分力は0になります。この状態を「自由落下」といいます。
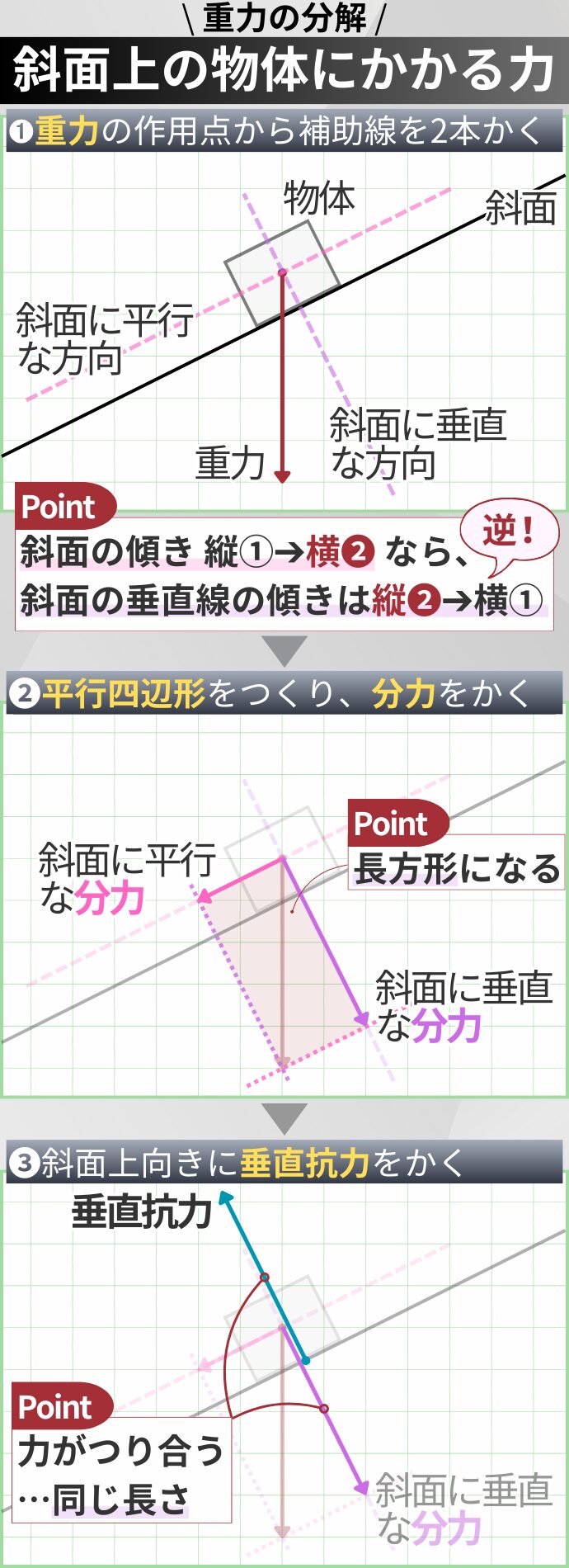
斜面上の物体は、斜面に対してすべり下りるだけでなく、斜面を垂直に押しています。これに対し、斜面が物体を押し返す力を垂直抗力といいます。
「斜面に垂直な分力」と、斜面が物体を支える「垂直抗力」は、つねにつり合っています。
※注意※
分力のもとの力は重力なので、地球が物体を引く力。垂直抗力は斜面が物体を押す力。1つの物体にはたらく2力のつり合いであって、作用・反作用ではありません。
よくある質問(FAQ)
Q. 2人で荷物を引き上げるとき、できるだけ小さな力にするにはどうすればいい?
A. 2人の間の角度を小さくする(2人が近づいて引く)と、小さな力で荷物を引き上げられます。
もとの2力の角度が小さいほど、合力は大きくなるためです。0°のとき、合力は最大になります。
2人で荷物をもつときは、なるべく近づくと一人一人の引く力を小さくできます。
Q. 身のまわりにある道具やもので、力の分解を利用したしくみや工夫があるものって?
A. つり橋を支えるワイヤー、まき割りのなたや斧、ハンモック、ジェットコースターなどがあります。
まとめ:力の合成・分解の重要ポイント
この記事では、中学3年生で学習する「力の合成と分解」について、作図のポイントを中心に解説しました。
- 力の合成は、複数の力を1つの力(合力)にまとめること。作図では、2力を2辺とする平行四辺形の対角線が合力になる
- 力の分解は、1つの力を2つ以上の力(分力)に分けること。作図では、もとの力を対角線とする平行四辺形の2辺が分力になる
- 作図問題を解くには、三角定規をヨットに見立てるか、方眼紙のマス目を読み取る
作図のルールさえ覚えてしまえば、力の合成・分解は必ず得意分野にできます。
「力の合成・分解」は、高校物理の基礎にもつながる、とても大切な考え方です。








